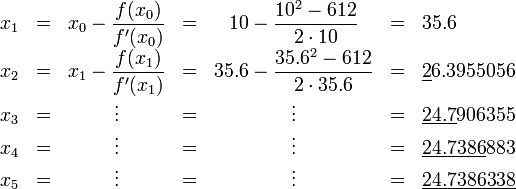Chapter 2 Solution of Non Linear Equation

September 11, 2008 sutanto
Off
Metode Numerik

Modul Silakan download disini Bisection methode metnum page 11_16

BISECTION METHODE

Metode biseksi ini adalah metode untuk mencari akar-akar dari sebuah fungsi dengan cara menghitung nilai fungsi f(x) dari 2 nilai X : (X1,X2) yang diberikan, dan diharapkan nilai f(X1).f(X2)< 0. Jika kedua nilai fungsi tersebut masih negatif untuk setiap X1 dan X2 yang diberikan, maka X3 ditentukan dengan menghitung rata-rata antara X1 dan X2. Jadi Xmid=(X1+X2)/2. Hitung f(Xmid), carilah pasangan yang menunjukan bahwa f(Xmid).f(X1) atau f(Xmid).F(X2) yang berniai negatif. Jika f(Xmid).F(X2)<0, maka interasi berikutnya adalah mencari X mid baru = (Xmid + X2)/2

Fresh Idea : Roots (akar-akar) sering ditulis X1 dan X2 dalam persamaan kuadrat. Bagaimana menentukan siapa yang disebut sebagai X1 dan sebagai X2? Apakah yang paling dekat dengan Nol disebut X1 ataukah yang paling kiri disebut sebagai X1? kayaknya kesepakatan ini belum pernah dirumuskan. Kok repot dengan nama….kenapa? Karena akan mempengaruhi banyak hal. Misal diketahui X1-X2=1 bila akar2nya negatif Coba pikirkan X1 adalah yang paling kiri atau yang terdekat dengan Nol?

Fresh Idea Application of Bisection method : Example aplikasi atau terapan Roots pada Bisection Methode adalah pada proses lelang forward sebuah barang. Antara penjual dan pembeli yang saling menawar untuk menuju harga kesepakatan. Harga kesepakatan adalah akar yang dicari dan akan dapat dibangun fungsi penawaran harga dari penjual dan pembeli dari masing masing penawaran harga. Kenapa lelang sama dengan bisection method, karena konsistensi f(X1)f(x2)<0 terjaga artinya tidak mungkin seorang pembeli menawar harga barang cenderung turun nilainya , pasti menuju naik menuju harga kesepakatan. Demikian juga dengan seorang penjual dalam memberikan harga penawaran.

Ada hal yang menarik dari event lelang komoditi ini. Yaitu pergerakan penawaran harga dari penjual dan pembeli. Pergerakannya sangat berbeda antara barang/ komoditi agro dan barang antik. Untuk referensi yg fresh diharapkan mahasiswa mengunjungi http://komoditi.jateng.go.id dan mengunjungi pasar lelang agro di Soropadan Pringsurat Temanggung pada setiap 2 bulan sekali.

===================================================================

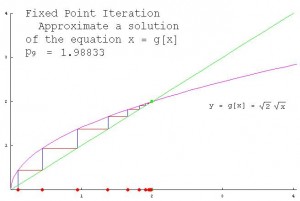
FIXED POINT INTERATION

Fixed Point ini hanya mengandalkan merubah bentuk fungsi dengan tidak merubah nilai. Fungsi aslinya f(X) = 0 dirubah dalam bentuk X=G(X). Sehingga bentuk X=G(X) akan memberikan interasi nilai X1, X2, …dst sampai dengan Xr sebagai akar-akar yang diinginkan.

Fresh Idea Application of Fixed Point Interation : Perusahaan Taksi KOSTI di Solo sedang menghadapi masalah yaitu : setoran Rp 190.000,- per hari akhri-akhir ini sulit untuk dipenuhi oleh para karyawannya (sopir taksi). Kenapa ? 1) Persaingan antar Taksi terlalu ketat. 2) Ternyata sebagian besar dari mereka habis pemasukannya untuk biaya operasional (mobilitas yang tinggi sebelum dapat penumpang). Mereka punya data taksi dipesan dari mana dan oleh siapa serta mau kemana. Data itu ditulis pakai tangan secara manual. Ini penyebab awal petaka perusahaan. Mereka tidak pernah belajr dari data. Karena data itu akan sulit dibaca dan dianalisa serta ternyata database itu hanya dipakai kalau terjadi penumpang komplain : Barangnya ketinggalan di Taksi.

Padahal data itu akan dengan mudah menjelaskan pergerakan penumpang yang meminta Taksi dan menuju kemana penumpang tersebut. Sehingga dengan data itu sebenarnya bisa dipakai untuk penentuan pakalan taksi yang paling tepat (untuk menghindari mobilitas Taksi kosong yang tinggi). Nah dalam menentukan titik koordinat pangkalan taksi itu Fixed Point Interation bisa diaplikasikan.

Silakan download disini fixed point methode

Untuk melihat animasi silakan klik klink berikut : http://www.ecs.fullerton.edu/~mathews/a2001/Animations/RootFinding/FixedPoint/Fixpointaa.html

Note : Korelasi antara gradien garis singgung di g(x) dimana g'(x) < 1pada fixed point methode dengan f'(x) pada newton methode

====================================================================

Modul newton raphson silakan download disini 21_24

Newton Methode

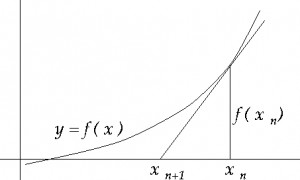
Bahwa Kurva itu dibentuk atau dibangun dari kumpulan garis singgung. Dari Garis singgung diperoleh gradien garis singgung pada saat menyinggung kurva di titik Xn. Dari Gradien garis singgung diperoleh nilai Xn+1 dengan memasukan pada rumus berikut :

Xn+1 = Xn – [f(Xn)/f ‘(Xn)]


Fresh Idea aplikasi Newton Methode adalah pengamatan pesawat terbang yang melakukan landing dan atau tinggal landas. Ketika akan landing, Keputusan pilot untuk mengurangi ketinggian dan kecepatan pesawat setiap menit hingga ban pesat menyentuh landasan adalah sesungguhnya merupakan interasi gerakan nilai akar-akar dari sebuah kurva dalam methode Newton.

Metode Babylonian kasus khusus dari metode Newton untuk menentukan akar adalah Metode Babilonia. Bisa jadi dari sinilah ide memperluas definisi akar : square roots

Berikut adalah cara Newton mencari √612 dengan memberi nilai awal 10 :

\begin{matrix} x_1 & = & x_0 - \dfrac{f(x_0)}{f'(x_0)} & = & 10 - \dfrac{10^2 - 612}{2 \cdot 10} & = & 35.6 \quad\quad\quad{} \\ x_2 & = & x_1 - \dfrac{f(x_1)}{f'(x_1)} & = & 35.6 - \dfrac{35.6^2 - 612}{2 \cdot 35.6} & = & \underline{2}6.3955056 \\ x_3 & = & \vdots & = & \vdots & = & \underline{24.7}906355 \\ x_4 & = & \vdots & = & \vdots & = & \underline{24.7386}883 \\ x_5 & = & \vdots & = & \vdots & = & \underline{24.7386338} \end{matrix}

dari iterasi diatas nampak nilai dari √612 konvergen menuju 24.7386

Metode Numerik
Metode Numerik